Análisis no-lineal de nudos de concreto sin refuerzo.

Resumen

Introducción- El Sistema estructural Pórticos de Concreto Reforzado (PCR) constituye una parte significativa del inventario de edificaciones en zonas sísmicamente activas en el mundo. Muchas de las edificaciones construidas antes de la década de los 80’s fueron diseñadas y construidas con poca, o ninguna consideración de cargas sísmicas. Cuando el nudo de concreto reforzado no se ha diseñado competentemente puede convertirse en el eslabón débil del sistemas de PCR. La presencia de nudos sin refuerzo, aun es común en países emergentes localizados en Asia y América Latina. Los nudos tienen un impacto significativo en el comportamiento de PCR. Las metodologías relacionadas con el análisis de nudos de concreto pueden catalogarse como aproximadas, o muy complejas, o de enfoque fenomenológico. Desafortunadamente la mayoría de ellas carece de la simplicidad, estabilidad, y practicidad requerida para evaluar el comportamiento de los nudos en PCR.  Este artículo presenta una alternativa analítica aplicable a este tipo de elementos estructurales.

Objetivo- El propósito del presente artículo es presentar un método analítico modificado aplicable al análisis no lineal de nudos no reforzados en estructuras de PCR.

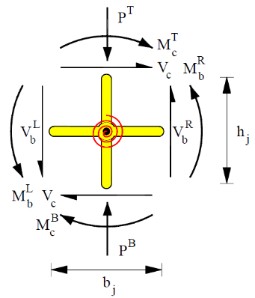
Metodología- El método presentado se basa en el trabajo analítico y experimental encontrado en [1], el cual es modificado para seguir exactamente la nomenclatura de [2]. En el modelo analítico, el nudo es representado a través de: (1) elementos rígidos en cruz para idealizar la geometría del nudo, (2) un resorte rotacional con una curva empírica de comportamiento tetra-lineal localizado en la mitad de los elementos rígidos para representar el comportamiento en cortante del nudo, y (3) las vigas y columnas que llegan al nudos, son modeladas con análisis seccional basado en fibras, con 5 puntos de integración; con la finalidad de incorporar el comportamiento no-lineal de los elementos que llegan al nudo. El modelo propuesto fue implementado en la plataforma OpenSEES y al mismo tiempo se validó con el resultado de 13 ensayos de laboratorio encontrados en la literatura de nudos carentes de acero de refuerzo.

Resultados- El modelo propuesto puede capturar adecuadamente la capacidad a cortante del nudo. Al comparar los resultados analíticos con 13 resultados de nudos de concreto encontrados en la literatura, se encontró una diferencia en la capacidad del 2% con una desviación estándar del 11%. En relación al comportamiento del nudo ante carga cíclica se observó que se captura en forma adecuada: la rigidez inicial, resistencia, degradación de la resistencia, rigidez de recarga y capacidad antes y después del pico de resistencia.

Conclusiones- El método propuesto presenta una adecuada correlación con los resultados de laboratorio estudiados. La metodología propuesta competentemente captura la capacidad del nudo a cortante, a pesar de las modificaciones incorporadas, sin mencionar las incertidumbres asociadas a los materiales, resultados de laboratorio, y tolerancias. Se espera que el procedimiento presentado en el presente documento contribuya, de una forma práctica, en la incorporación de la flexibilidad del nudo en PCR diseñados primariamente para cargas gravitacionales.