A multi-objective optimization of contamination al-gorithm for a contaminated region

Abstract

Introduction: This work considers an industrial ecology problem under the framework of semi-infinite optimization.

Objective: The objective is to resolve the conflict between pollutant emissions and environmental standards for the areas within a given region.

Methodology: A version of the SIP2 algorithm is proposed, which simultaneously allows for a reduction in pollution while also enabling an increase in emissions from sources. This approach provides a certain degree of flexibility in managing pollution and the factors that cause it in the industry, while ensuring compliance with environmental regulations.

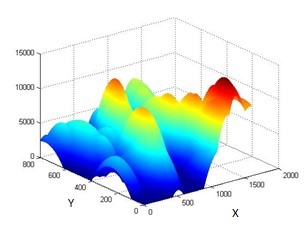
Results: The results of two algorithms show different roles of the sources in obtaining the total pollution and, therefore, the need for changes in their emissions.

Conclusions: The proposed algorithm offers more cost-effective solutions in infrastructure design evaluations for areas with conflicting interests, such as maintenance or increasing production (indirectly measured by emissions generated from the production system), while ensuring compliance with restrictive environmental regulations.