Voracious and Heuristic Algorithms: A focus on the Minimum Path Problem
DOI:
https://doi.org/10.17981/10.17981/ingecuc.16.2.2020.05Keywords:
weighted graph, cost matrix, adjacency matrix, optimal route, voracious algorithms, greedy search, heuristics, Greedy, A-star, DijkstraAbstract
Introduction— The problem of the shortest route or minimum cost route, has been one of the topics most studied by areas of knowledge such as Operations Research, Computer Science and Decision, Telecommunications, Plant Distribution, Planning of Projects, among others, searching, for example: optimize and reduce the costs that represent the distribution of goods, obtain the minimum amount of time necessary to complete a project, or calculate the shortest possible route between computers connected to a network.
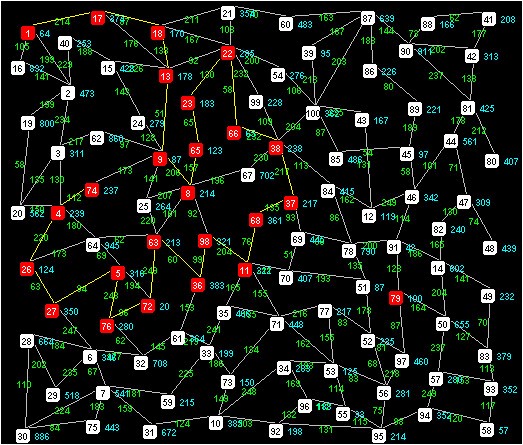
Objective— We will study the behavior of three voracious algorithms that allow us to calculate the minimum cost route between two points (initial state and objective state) in a weighted graph and with heuristics.
Methodology— Was implemented in Java, and the Greedy, A* and Dijkstra algorithms were adjusted to the problem in question. Subsequently, two instance cases were designed, one negative and one positive.
Results— In the negative instance results the heuristic of the node was modified to allow the selected algorithm to escape from local optima and thus obtain a complete result, that is to say reach the objective state, which, in some cases, will not necessarily be the most optimal result.
Conclusions— By comparing the three algorithms, it was determined that the Dijkstra algorithm always yields complete and optimal results. For its part, Greedy and A*, need heuristics to reach a complete result, but not optimal.
Downloads
References
N. Ojekudo & N. Akpan, “Anapplication of Dijkstra’s Algorithm to shortest route problem”, IOSR-JM, vol. 13, no. 3, pp. 20–32, 2017. Available: http://iosrjournals.org/iosr-jm/pages/v13(3)Version-1.html
B. Obregón, “Teoría de redes: El problema de la ruta más corta”, tesis magistral, prog. ing., UNAM, CDMX, MX. 2005. Available at: http://www.ptolomeo.unam.mx:8080/xmlui/bitstream/handle/132.248.52.100/539/obregonquintana.pdf?sequence=12
J. Barelles, “Algoritmos para la resolución de problemas en redes”, trabajo grado, dpto Mat Comp, UJI, Cast, Esp, 2017. Available from http://repositori.uji.es/xmlui/bitstream/handle/10234/173687/TFG_2017_BarellesMenes_Jorge.pdf?sequence=1&isAllowed=y
Y. Talebiy & H. Rashmanlouz, “Application Of Dominating Sets In Vague Graphs”, Appl Math E-Notes, vol. 17, pp. 251–267, 2017. Available from https://www.emis.de/journals/AMEN/2017/AMEN-170503.pdf
M. Dod, “Domination in graphs with application to network reliability”, Thesis Doctor, Fac Math Comp Sci, FUMT, Fog, DE, 2015. Available from https://tubaf.qucosa.de/api/qucosa%3A23011/attachment/ATT-0/
S. Guze, “An application of the selected graph theory domination concepts to transportation networks modelling”, Zesz Nauk Uniw Rzesz, vol. 52, no. 124, pp. 97–102, 2017. https://doi.org/10.17402/250
S. Vishwanathan, N. Schraudolph, R. Kondor & K. Borgwardt, “Graph Kernels”, JMLR, vol. 11, pp. 1201–1242, 2010. Available from http://www.jmlr.org/papers/volume11/vishwanathan10a/vishwanathan10a.pdf
K. Abdulkalek & A. Kilicman, “Topologies on the Edges Set of Directed Graphs”, Int J Math Anal, vol. 12, no. 2, pp. 71–84, 2018. https://doi.org/10.12988/ijma.2018.814
N. Jicy & M. Sunil, “Some new connectivity parameters for weighted graphs”, J Uncertain Math Sci, pp. 1–9, 2014. Available: https://www.researchgate.net/publication/263773151_Some_new_connectivity_parameters_for_weighted_graphs_Some_new_connectivity_parameters_for_weighted_graphs
A. Ban, “Decomposing Weighted Graphs”, JGT, vol. 86, no. 2, pp. 250–254, 2017. https://doi.org/10.1002/jgt.22124
S. Mathew, “Partial trees in weighted graphs-I”, Proyecciones J Math, vol. 30, no. 2, pp. 163–174, 2011. http://dx.doi.org/10.4067/S0716-09172011000200003
C. Salas, “Un Algoritmo de Dos Fases para la Optimización de Costos en el Traslado de Cargas con Exceso de Dimensiones”, Tesis magistral, UAEH, HGO, MX, 2014. Disponible en http://dgsa.uaeh.edu.mx:8080/bibliotecadigital/bitstream/handle/231104/1918/AT18381.pdf?sequence=3&isAllowed=y
G. González & F. González, “Metaheurísticas aplicadas al ruteo de vehículos. Un caso de estudio. Parte 2: algoritmo genético, comparación con una solución heurística”, Rev Ing Inv, vol. 27, no. 1, pp. 149–157, 2007. Available from https://revistas.unal.edu.co/index.php/ingeinv/article/view/14795/15626
L. Rodríguez & A. Varona. Técnicas de diseño de algoritmos. Algoritmos voraces. (2015). Curso de informática. PV, Esp: UPV. Recuperado de https://ocw.ehu.eus/pluginfile.php/46102/mod_resource/content/1/03_Algoritmos_Voraces/03_Algoritmos_Voraces.pdf
A. Subhadra, “Greedy Algorithms: Analysis, Design & Applications”, IJIFR, vol. 3, no. 5, pp. 1749–1764, 2016. Available: https://www.academia.edu/21855750/Greedy_Algorithms_Analysis_Design_and_Applications
D. Maxwell, “Optimal Structure Identification With Greedy Search”, JMLR, vol. 3, pp. 507–554, 2002. Available: https://www.jmlr.org/papers/v3/chickering02b.html
B. Simmons, C. Hoeppke & W. Sutherland, “Sutherland. Beware greedy algorithms”, J Anim Ecol, vol. 88, no. 5, pp. 804–807, 2019. https://doi.org/10.1111/1365-2656.12963
A. Malik, A. Sharma & V. Saroha, “Greedy Algorithm”, IJSRP, vol. 3, no. 8, pp. 1–5, 2013. Available: http://www.ijsrp.org/research-paper-0813.php?rp=P201564
O. Debdi, “Aprendizaje Interactivo de Algoritmos Voraces: del Enfoque Individual al Colaborativo”, Tesis Doctoral, URJC, MD, ES, 2014. Available: http://hdl.handle.net/10115/13242
U. Faigle, “The greedy algorithm for partially ordered sets”, Discrete Math, vol. 28, no. 2, pp. 153–159, 1979. https://doi.org/10.1016/0012-365X(79)90092-X
M. Abad. Algoritmos voraces, Anàlisi i Disseny d’Algorismes. (2007-2008). Curso de informática. BCN, ES: UPC. Available from http://www.cs.upc.edu/~mabad/ADA/curso0708/GREEDY.pdf
N. Shrikant & A. Selvakumar, “Implementation of A* Algorithm to Autonomous Robots-A. Simulation Study”, Eng Technol Open Acc, vol. 1, no. 3, pp. 88–91, 2018. https://doi.org/10.19080/ETOAJ.2018.01.555564
P. Sudhakara & V. Ganapathy, “Trajectory Planning of a Mobile Robot using Enhanced A-Star Algorithm”, Indian J Sci Technol, vol. 9, no. 41, pp. 1–10, 2016. https://doi.org/10.17485/ijst/2016/v9i41/93816
J. Peng, Y. Huang & G. Luo, “Robot Path Planning Based on Improved A* Algorithm”, Cybern Inf Technol, vol. 15, no. 2, pp. 171–180, 2015. https://doi.org/10.1515/cait-2015-0036
R. Rodríguez-Puente & M. Lazo-Cortés, “Búsquedas de caminos mínimos haciendo uso de grafos reducidos”, Ing Ind, vol. 38, no. 1, pp. 32–42, 2017. Available at: https://rii.cujae.edu.cu/index.php/revistaind/article/view/497/759
F. Duchon, A. Babineca, M. Kajana, P. Beño, M. Florek, T. Fico & L. Jurišica, “Path planning with modified A star algorithm for a mobile robot”, Procedia Manuf, vol. 96, pp. 59–69, 2014. https://doi.org/10.1016/j.proeng.2014.12.098
X. Dai, S. Long, Z. Zhang & D. Gong, “Mobile Robot Path Planning Based on Ant Colony Algorithm With A* Heuristic Method”, Front Neurorobot, vol. 13, pp. 1–9, 2019. https://doi.org/10.3389/fnbot.2019.00015
A. KumarGuruj, H. Agarwal & D. Parsediya, “Time-Efficient A* Algorithm for Robot Path Planning”, Procedia Technol vol. 23, pp. 144–149, 2016. https://doi.org/10.1016/j.protcy.2016.03.010
A. Beriain, “Matemáticas en un Navegador GPS: Algoritmos de Camino más Corto y Calculo de Posición”, trabajo grado, UR, LR, Esp, 2016. Available from https://biblioteca.unirioja.es/tfe_e/TFE002201.pdf
M. Nosrati, R. Karimi & H. Hasanvand, “Investigation of the * (Star) Search Algorithms: Characteristics, Methods and Approaches”, World Appl Program, vol. 2, no. 4, pp. 251–256, 2012. Available at: https://pdfs.semanticscholar.org/831f/f239ba77b2a8eaed473ffbfa22d61b7f5d19.pdf
N. Gupta, K. Mangla, A. Kumar & M. Umar. “Applying Dijkstra’s Algorithm in Routing Process”, IJNTR, vol. 2, no. 5, pp. 122–124, 2016. Available from https://www.ijntr.org/download_data/IJNTR02050040.pdf
Published
How to Cite
Issue
Section
License
Copyright (c) 2020 INGE CUC

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published papers are the exclusive responsibility of their authors and do not necessary reflect the opinions of the editorial committee.
INGE CUC Journal respects the moral rights of its authors, whom must cede the editorial committee the patrimonial rights of the published material. In turn, the authors inform that the current work is unpublished and has not been previously published.
All articles are licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.


 English
English
 Español (España)
Español (España)






















