Production line balancing in the pharmaceutical industry using Goal Programming
DOI:
https://doi.org/10.17981/ingecuc.15.1.2019.10Keywords:
line balancing, cycle time, goal programming mathematical model, multi-objective approachAbstract
Introduction: In a production Line it’s important that the stations’ cycle times are balanced and that they are low since this allows to reduce the work in process. However, doing this leads to an increase in the stations’ number, that is not favorable because it raises the costs associated with the stations, therefore it is necessary to define strategies that allow achieving a balance between these requirements.
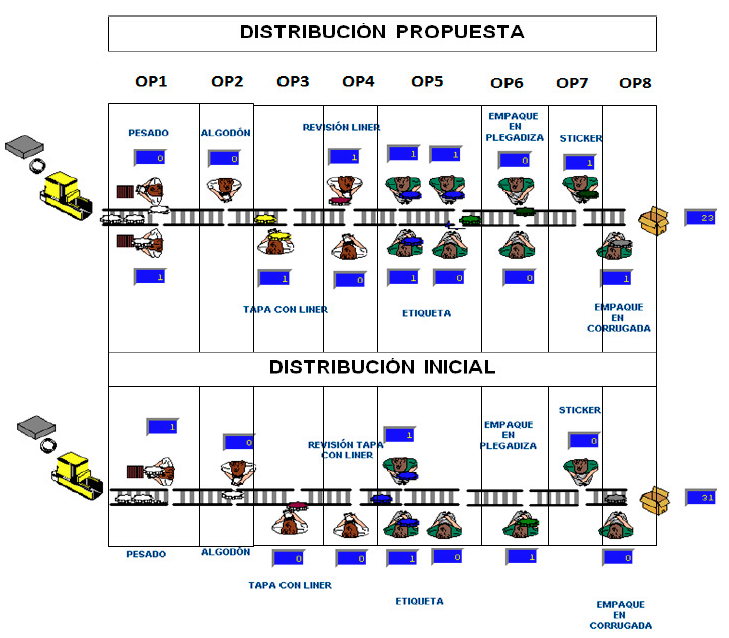
Objective: In this article we propose the formulation of a model for the line balancing, using the technique of multi-objective goal programming, applied to the pharmaceutical industry in order to minimize the stations’ number, minimize cycle time and inventory in process.
Methodology: Goal programming is used to address a line balance model, which considers at the same time the assignment of multiple stations to one operation and the assignment of multiple operations to one station.
Results: A significant decrease in cycle time and idle time at minimum costs is achieved, and a comparison between the deterministic and stochastic models is presented.
Conclusions: Through this implementation of the LINGO model, the compliance of the proposed restrictions, the precedence of operations and the proper functioning of the model were validated through the optimal solutions obtained. The simulation is a tool that illustrates the complexity of the operations of the production system, which require, as in our case, more realistic modeling to understand the behavior of the process and evaluate different strategies.
Downloads
References
N. Boysen, M. Fliedner and A. Scholl, “A classification of assembly line balancing problems,” Eur. J. Oper. Res., vol. 183, no. 2, pp. 674–693, Dec. 2007, doi: https://doi.org/10.1016/j.ejor.2006.10.010
J. Pereira and E. Álvarez-Miranda, “An exact approach for the robust assembly line balancing problem,” Omega, vol. 78, pp. 85–98, Jul. 2018, doi: https://doi.org/10.1016/j.omega.2017.08.020
I. Baybars, “A Survey of Exact Algorithms for the Simple Assembly Line Balancing Problem,” Manage. Sci., vol. 32, no. 8, pp. 909–932, Aug. 1986, doi: https://doi.org/10.1287/mnsc.32.8.909
E. Erel, “A study on production lines with discrete batch WIP inventory transfer,” Int. J. Prod. Econ., vol. 55, no. 1, pp. 71–85, Jun. 1998, doi: https://doi.org/10.1016/S0925-5273(98)00042-5
E. Erel, “Effect of discrete batch WIP transfer on the efficiency of production lines,” Int. J. Prod. Res., vol. 31, no. 8, pp. 1827–1838, Aug. 1993, doi: https://doi.org/10.1080/00207549308956825.
P. J. Egbelu and N. Roy, “Material flow control in AGV/unit load based production lines,” Int. J. Prod. Res., vol. 26, no. 1, pp. 81–94, Jan. 1988, doi: https://doi.org/10.1080/00207548808947842
P. J. Egbelu, “Batch production time in a multi-stage system with material-handling consideration,” Int. J. Prod. Res., vol. 29, no. 4, pp. 695–712, Apr. 1991, doi: https://doi.org/10.1080/00207549108930096
P. J. Egbelu, “Machining and material flow system design for minimum cost production,” Int. J. Prod. Res., vol. 28, no. 2, pp. 353–368, Feb. 1990, doi: https://doi.org/10.1080/00207549008942716
R. G. Qiu, “Virtual production line based WIP control for semiconductor manufacturing systems,” Int. J. Prod. Econ., vol. 95, no. 2, pp. 165–178, Feb. 2005, doi: https://doi.org/10.1016/j.ijpe.2003.12.004
W. Choi and Y. Lee, “A dynamic part-feeding system for an automotive assembly line,” Comput. Ind. Eng., vol. 43, no. 1–2, pp. 123–134, Jul. 2002, doi: https://doi.org/10.1016/S0360-8352(02)00071-2
A. Scholl and R. Klein, “SALOME: A Bidirectional Branch-and-Bound Procedure for Assembly Line Balancing,” INFORMS J. Comput., vol. 9, no. 4, pp. 319–334, Nov. 1997, doi: https://doi.org/10.1287/ijoc.9.4.319
P. R. McMullen and P. Tarasewich, “Multi-objective assembly line balancing via a modified ant colony optimization technique,” Int. J. Prod. Res., vol. 44, no. 1, pp. 27–42, Jan. 2006, doi: https://doi.org/10.1080/00207540500216748
A. Scholl and C. Becker, “State-of-the-art exact and heuristic solution procedures for simple assembly line balancing,” Eur. J. Oper. Res., vol. 168, no. 3, pp. 666–693, Mar. 2006, doi: https://doi.org/10.1016/j.ejor.2004.07.022
Y. Bukchin and T. Raviv, “Constraint programming for solving various assembly line balancing problems,” Omega, vol. 78, pp. 57–68, Jul. 2018, doi: https://doi.org/10.1016/j.omega.2017.06.008
J. Pereira and E. Álvarez-Miranda, “An exact approach for the robust assembly line balancing problem,” Omega, vol. 78, pp. 85–98, Jul. 2018, doi: https://doi.org/10.1016/j.omega.2017.08.020
J. R. Coronado-Hernandez and H. Ospina-Mateus, “Incorporación de Riesgos Ergonómicos en el Balanceo de Líneas de Ensamble en U,” WPOM - Work. Pap. Oper. Manag., vol. 4, no. 2, pp. 29–43, Sept. 2013, doi: http://dx.doi.org/10.4995/wpom.v4i2.1164
E. H. Bowman, “Assembly-Line Balancing by Linear Programming,” Oper. Res., vol. 8, no. 3, pp. 385–389, Jun. 1960. doi: http://dx.doi.org/10.1287/opre.8.3.385
C. N. Klahr, “Multiple Objectives in Mathematical Programming,” Oper. Res., vol. 6, no. 6, pp. 849–855, Nov. 1958. Available: https://doi.org/10.1287/opre.6.6.849
A. Charnes and W. W. Cooper, Management models and industrial applications of linear programming, vol. 1, N.J., USA: John Wiley & Sons, 1961.
Y. Ijiri, Management goals and accounting for control, Haarlem, Netherlands: North Holland Pub. Co., 1965.
F. S. Hillier and G. J. Lieberman, Investigación de operaciones, 10th ed., Madrid, España: McGraw-Hill Interamericana S.L., 2016.
C. Romero, “El enfoque multiobjetivo en los modelos matemáticos de planificación de cultivos,” Rev. Econ. Polit., vol. 89, pp. 179–204, Sept. 1981.
S. M. Lee, Goal Programming for Decision Analysis, Philadelphia, USA: Auerbach Pub., 1972.
J. P. Ignizio, Goal programming and extensions, Toronto, Canada: Lexington Books, 1976.
C. Romero, Análisis de las decisiones multicriterio, vol. 14, Madrid, España: Isdefe, 1996.
Ö. Polat, Ö. Mutlu and E. Özgörmüş, “A Goal Programming Model For Assembly Line Balancing Problem Type 2 Under Workload Constraint.” in The 2015 Northeast Decision Sciences Conf., Cambridge, MA, March 2015.
M. C. O. Moreira, R. Pastor, A. M. Costa and C. Miralles, “The multi-objective assembly line worker integration and balancing problem of type-2,” Comput. Oper. Res., vol. 82, pp. 114–125, Jun. 2017, doi: https://doi.org/10.1016/j.cor.2017.01.003
A. J. R. Smith and A. Bhandari, “Multiple criteria approach to the stochastic assembly line balancing problem,” Proc. 33rd Int. Matador Conf., 2000, pp. 61–66.
O. Rosenberg and H. Ziegler, “A comparison of heuristic algorithms for cost-oriented assembly line balancing,” ZOR Zeitschrift fü Oper. Res. Methods Model. Oper. Res., vol. 36, no. 6, pp. 477–495, Nov. 1992. Available: https://link.springer.com/article/10.1007/BF01416240
Published
How to Cite
Issue
Section
License
Copyright (c) 2019 INGE CUC

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published papers are the exclusive responsibility of their authors and do not necessary reflect the opinions of the editorial committee.
INGE CUC Journal respects the moral rights of its authors, whom must cede the editorial committee the patrimonial rights of the published material. In turn, the authors inform that the current work is unpublished and has not been previously published.
All articles are licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.


 English
English
 Español (España)
Español (España)






















